How Do Microphones Work?Mechanical Wave Energy & Sound WavesElectrical Energy & Audio SignalsWaveformsAmplitudeFrequencyHow Sound WorksHarmonicsAdditive SynthesisSignalsHow is sound stored in the computer?Types of SignalsAnalog-to-Digital ConversionDigital-to-Analog ConversionOther characteristics of signalFundamental FrequencyWhat Audio Formats are Used?SpectrogramsFourier TransformDiscrete Fourier TransformDiscrete Fourier Transform Errors & Short-time Fourier TransformFast Fourier Transform Spectrogram GenerationSpectrogram AlternativesCepstrumFeaturesMFCCsDown-sampling the log-spectrumMel-scaleMFCCsSources
How Do Microphones Work?
- Microphones function as transducers.⇒ Convert sound waves (mechanical wave energy) into audio signals (electrical energy):
Mechanical Wave Energy & Sound Waves
- Mechanical wave energy is the energy carried by the oscillation of matter in a medium (mechanical wave).
- Sound wave is a type of mechanical wave caused by the disturbance of particles within an elastic medium, such as gas (air), liquid (water), or solid.
- Sound waves oscillate within a range of Loading equation...Hz.
- Infrasound occurs below Loading equation...Hz (inaudible to humans), while ultrasound occurs aboveLoading equation...Hz.
- Sound waves oscillate within a range of
Electrical Energy & Audio Signals
- Electrical energy refers to electric potential energy.
- In modern times, we harvest electrical energy and convert it into other types of energy.
- An audio signal is an electrical signal that represents sound in the form of electrical energy.
- Measured as AC voltages in millivolts (RMS) or in decibels relative to voltage (dBV or dBu).
Waveforms
- A waveform is a graph that shows the displacement of air molecules over time as a sound wave travels.
- X-axis represents time:
- Y-axis measures displacement of air molecules:
- NB: this displacement measures the sound wave's loudness.
- E.g.: A lightly strummed guitar string only vibrates slightly, causing a small displacement. If you pull the string back by an inch and release, it vibrates more, causing a larger displacement and a louder sound.
- NB: this displacement measures the sound wave's loudness.
- The waveform graph above shows one complete oscillation of a sound wave.
- It starts by displacing the air molecules positively (+1) and then negatively (-1).
- X-axis represents time:
Amplitude
- Waveforms are abstract representations of sound waves.
- While real sound waves may displace air molecules by Loading equation...nanometers, we use abstract measurements for waveforms.
- While real sound waves may displace air molecules by
- Amplitude measures how much a molecule is displaced from its resting position.
- We measure from Loading equation...(silence) toLoading equation...(maximum displacement).
- A waveform's amplitude controls the maximum displacement.
- The higher the amplitude, the louder the sound; the lower the amplitude, the quieter the sound.
- We measure from
Frequency
- In periodic waveforms, frequency is key:
- Frequency measures how many times a waveform repeats within a given time.
- The common unit for frequency is Hertz (Hz), representing the number of repetitions per second.
- E.g.: the waveform above shows a Loading equation...-second interval. This wave oscillates at 2 Hz.
- E.g.: the waveform above shows a
- Frequency is closely related to pitch:
- E.g.: a singer singing an "A4" note vibrates their throat at 440 Hz. When singing "C5" (3 semitones higher), their throat vibrates at 523 Hz.
⇒ The faster a wave repeats, the higher the pitch; the slower, the lower the pitch.
- Not all sounds are periodic, though:
- White noise contains all audible frequencies, distributed uniformly.⇒ Because white noise is not periodic, it has no discernible pitch.
- White noise contains all audible frequencies, distributed uniformly.
How Sound Works
- The air around us contains molecules. When an object vibrates, it causes nearby molecules to vibrate. These molecules impact neighboring ones, propagating the wave outward from the source until its amplitude (volume) fades with distance. The vibration moves through air molecules like a chain reaction, eventually reaching your ear, where your brain interprets it as sound.
- NB: the air molecules do not move across space; they only vibrate.
- On Earth, sound travels primarily through air, but it can also travel through water or solid ground (like the rumble of an earthquake). The farther the molecules move with each pulse, the higher the amplitude (volume) of the sound. The faster they vibrate, the higher the frequency (pitch).
Harmonics
- The shape of a waveform describes how the displacement changes over time.
- The sine waveform is known as the fundamental waveform because it is pure and has no harmonics.⇒ With such form, there are no "side effects": it doesn't have any bells or whistles.⇒ When you play a 440 Hz sine wave, the only frequency you hear is 440 Hz.
- The sine waveform is known as the fundamental waveform because it is pure and has no harmonics.
- When a waveform has "side effect" frequencies, we call them harmonics.
- Harmonics are additional frequencies that certain waveforms produce.
- E.g.: triangle waveforms only have odd harmonics.
- E.g.: square waveforms have the same harmonics as triangle waveforms, but their harmonics do not diminish as much with increasing frequency:
- NB: a perfect square wave cannot exist in nature because molecules cannot instantly "teleport" from +1 to -1. We can only approximate it.
- E.g.: sawtooth waveforms contain frequencies at every multiple of the fundamental frequency.
Frequency of 1Hz. 
Frequency of 2Hz. 
- E.g.: triangle waveforms only have odd harmonics.
- Harmonics are additional frequencies that certain waveforms produce.
Additive Synthesis
- A surprising fact about waveforms:All waveforms can be constructed by layering multiple sine waves on top of each other.
- Something counter-intuitive about waveform addition is that it does not always make the resulting sound louder. To demonstrate this more clearly, we have to learn about another waveform property—phase.
- Phase is the amount of offset applied to a wave, measured in degrees.
- This is exactly how noise-cancelling headphones work:
- NB: this process is imperfect: real noise is not as simple or consistent as sine waves.
- E.g.: can remarkably effect in areas with consistent low-frequency noise, like airplanes or subways.
⇒ There is latency between the sound being recorded and played back.⇒ Generally works better on lower-frequency noise where the latency matters less.
Record the ambient noise around the headphones.⇒ Offset its phase byLoading equation...degrees.⇒ Mix it in with the sound coming out of the headphone's speakers.⇒ This "cancels out" the background noise asLoading equation...-degree sine wave cancels out original sine wave. - NB: this process is imperfect: real noise is not as simple or consistent as sine waves.
⇒ If a wave is 180 degrees out of phase that means it's delayed by 50% of its period.
⇒ Add them together:
⇒ No sound at all. - This is exactly how noise-cancelling headphones work:
- Phase is the amount of offset applied to a wave, measured in degrees.
Signals
- Sound is air pressure fluctuations that microphones convert into electrical signals.
How is sound stored in the computer?
- In order to represent a sound wave in a way computers can manipulate and work with, the sound has to be converted into a digital form. This process is called analog to digital (A/D) conversion.
Types of Signals
- All signals fall into four categories:
- Analog signal — any continuous signal:
- Most physical processes are continuous over time. ⇒ Represent analog signals.
- The range of values and time is continuous.
- Most physical processes are continuous over time.
- Quantized signal — an analog signal with quantized values.
- The signal's values are divided into Loading equation...levels with a step sizeLoading equation....⇒ Each sample corresponds to a level.
- The signal's values are divided into
- Discrete signal — an analog signal sampled at discrete intervals.
- Represented as a sequence of values taken at discrete times Loading equation...with intervalLoading equation....
- Represented as a sequence of values taken at discrete times
- Digital signal — an analog signal that has undergone both quantization and discretization.
- The order of operations (quantization/discretization) doesn't matter.
- This is how sound is stored in a computer.
- Analog signal — any continuous signal:
Analog-to-Digital Conversion
- Process of converting an analog signal to a digital signal:
Basic parts of an A/D converter.
- A/D conversion process has the following form:
- Sampling takes samples of continuous-time signal at discrete-time instants.
- Analog signal is converted into digital form by a circuit that captures incoming wave's amplitude at regular intervals, converting data into a number in a form understood by the audio recording system.
- Each of these captured moments is a sample. ⇒ By chaining all the samples together, you can approximately represent the original wave.
- The more often you take samples of the original audio, the closer to original you can get.
- Number of samples taken per second is called the sample rate.
- Each of these captured moments is a sample.
- Analog signal is converted into digital form by a circuit that captures incoming wave's amplitude at regular intervals, converting data into a number in a form understood by the audio recording system.
- Quantization converts a discrete-time continuous-valued signal into discrete-time, discrete-valued signal.
- Coding reppresents each discrete value by a Loading equation...-bit binary sequence.
- Most audio files use 16-bit signed integers for each sample.
- But others might use 32-bit floating-point values or 24-bit or 32-bit integers.
- Size of an individual sample is called the sample size.
- Most audio files use 16-bit signed integers for each sample.
- Sampling takes samples of continuous-time signal at discrete-time instants.
- Position of each audio source within the audio signal is called a channel.
- Each channel contains a sample indicating the amplitude of the audio being produced by that source at a given moment in time.
- E.g.: in mono sound, there is only one audio source while in stereo sound, there are two audio sources: one speaker on the left, and one on the right. Each of these is represented by one channel, and the number of channels contained in the audio signal is called the channel count.
- Each channel contains a sample indicating the amplitude of the audio being produced by that source at a given moment in time.
Signal Sampling: Nyquist-Shannon Theorem
- The higher the sampling rate, or sampling frequency, the more accurate would be the stored information.
- E.g.: much higher sampling rate is needed for sampling a signal which is rich in high frequency components, such as the sound of music, compared to the sampling frequency needed for sampling a slowly varying signal, such as the output of a gas-chromatograph detector.
⇒ The more accurate would be the signal reconstruction from its samples.
- Loading equation...problem: high sampling rate produces a large volume of data to be stored.
- Q: Which is the minimum necessary sampling rate for a given type of signal, that will not distort the underlying information and/or allow its accurate reconstruction?
- E.g.: for digitalization of sound, a sampling rate of about Loading equation...kHz is sufficient for telephony, since normal human voice does not contain an appreciable amount of frequency components higher thanLoading equation...–Loading equation...kHz.
- E.g.: for digitalization of music, a sampling rate of about Loading equation...kHz is needed, since frequency components of aboutLoading equation...–Loading equation...kHz are common and needed for achieving fidelity of sound reconstruction.
- For digital recording of music in CD, a sampling rate of Loading equation...kHz is commonly used.
A: Nyquist-Shannon sampling theorem states that minimum sampling frequency of a signal that it will not distort its underlying information, should be double the frequency of its highest frequency component.⇒ In practice, the sampling rateLoading equation...is commonly selected in the rangeLoading equation.... - E.g.: for digitalization of sound, a sampling rate of about
- Q: Which is the minimum necessary sampling rate for a given type of signal, that will not distort the underlying information and/or allow its accurate reconstruction?
- Prior to sampling, signal must pass through a low-pass filter which will remove all unnecessary components higher than Loading equation..., preventing thus the "contamination" of the stored signal by their aliased frequencies.
Digital-to-Analog Conversion
- Process of converting a digital signal into an analog signal.
- Want to play back sound. ⇒ Amplitudes are used to generate an approximation of the original waveform.⇒ Instead of playing back an exact duplicate of the original, smooth wave, the rougher wave is played:
Zero-order hold D/A conversion.
- Use of interpolation by either:
- Connecting dots in a digital signal.
- Zero-order hold (staircase), linear, quadratic, and etc. approximations.
Other characteristics of signal
- Formally, signal is represented asLoading equation...whereLoading equation...— displacement of wave,Loading equation...— amplitude,Loading equation...— frequency,Loading equation...— phase.
- Power of a signal is Loading equation....
- Energy of a signal corresponds to the total magnitude of the signal:
- Roughly corresponds to how loud the signal is.
- In practice estimated by some window.
Loading equation...
Fundamental Frequency
- Fundamental frequency, Loading equation..., of a speech signal refers to the approximate frequency of the (quasi-)periodic structure of voiced speech signals.
- Oscillation originates from the vocal folds, which oscillate in the airflow when appropriately tensed. ⇒ Fundamental frequency is an average number of oscillations per second and expressed in Hz.
- Oscillation originates from an organic structure.
- Jitter — amount of variation in period length.
- Shimmer — amount of variation in amplitude.
⇒ It is not exactly periodic but contains significant fluctuations.
- Oscillation originates from the vocal folds, which oscillate in the airflow when appropriately tensed.
- Loading equation...is typically not stationary and changes constantly within a sentence.
- Lies roughly in the range from Loading equation...toLoading equation...Loading equation..., where males have lower voices than females and children.
- Loading equation...of an individual speaker depends primarily on the length of the vocal folds.⇒ They, in turn, correlated with overall body size.⇒ Cultural and stylistic aspects of speech naturally have also a large impact.
⇒ Can be used for expressive purposes to signify emphasis and questions. - Lies roughly in the range from
- Loading equation...is closely related to pitch, which is defined as our perception of fundamental frequency.
- Loading equation...describes the actual physical phenomenon.
- Pitch describes how our ears and brains interpret the signal in terms of periodicity.
- E.g.: voice signal could have an Loading equation...ofLoading equation.... If we then apply a high-pass filter to remove all signal components belowLoading equation..., then that would remove the actual fundamental frequency. The lowest remaining periodic component would beLoading equation..., which correspond to the fifth harmonic of the originalLoading equation.... However, a human listener would then typically still perceive a pitch ofLoading equation..., even if it does not exist anymore. The brain somehow reconstructs the fundamental from the upper harmonics. This well-known phenomenon is however still not completely understood.
- Speech signal with a fundamental frequency of approximately Loading equation...:
High-pass filtered version of it such that the fundamental frequency has been removed:
- Speech signal with a fundamental frequency of approximately
- If Loading equation...is the fundamental frequency, then the length of a single period in seconds is
- Example:
- NB: magnitude spectrum of Loading equation..., has then a periodic comb-structure.⇒ That is, the magnitude spectrum has peaks atLoading equation..., for integerLoading equation....
Segment of a speech signal, with the period length Loading equation..., and fundamental frequencyLoading equation....
Spectrum of speech signal with the fundamental frequency Loading equation...and harmonicsLoading equation..., as well as the formantsLoading equation...,Loading equation...,Loading equation..., etc. Notice how the harmonics form a regular comb-structure. - NB: magnitude spectrum of
Loading equation...⇒ Speech waveform thus repeats itself after everyLoading equation...seconds.⇒ Simple way of modeling the fundamental frequency is to repeat the signal after a delay ofLoading equation...seconds.⇒ If a signal is sampled with a sampling rate ofLoading equation..., then the signal repeats after a delay ofLoading equation...samples whereLoading equation...⇒ SignalLoading equation...then approximately repeats itself such thatLoading equation...⇒ In the Z-domain this can be modeled by an IIR-filter asLoading equation...where the scalarLoading equation...scales with the accuracy of the period.⇒ Z-transform of the signalLoading equation...can then be written asLoading equation...whereLoading equation...is the Z-transform of a single period.Spectrum of fundamental frequency modelLoading equation..., showing the characteristic comb-structure with harmonic peaks appearing at integer multiples ofLoading equation...:
- Example:
What Audio Formats are Used?
- Non-compressed formats: WAV, AIFF, etc.
- Lossless compression: FLAC, ALAC, etc.
- Lossy compression: MP3, Opus, etc.
Spectrograms
- Spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
- Common format is a graph with:
- Two geometric dimensions: one axis represents time, and the other axis represents frequency.
- Third dimension indicates the amplitude of a particular frequency at a particular time.
- Represented by the intensity or color of each point in the image.
- Common format is a graph with:
- It is bad to work with sound in raw format because:
- Raw audio signal is highly sensitive to various factors:
- Volume increase or decrease.
- External noise.
- Change in voice timbre.
⇒ This significantly affects model training quality, making them unstable due to overfitting. - One letter consists of Loading equation...–Loading equation...amplitudes.⇒ They are expensive to process and store.⇒ Using spectrograms can save memory.
- Raw audio signal is highly sensitive to various factors:
Fourier Transform
- Spectrograms may be created from a time-domain signal using the Fourier transform (FT).
- Video on the FT:
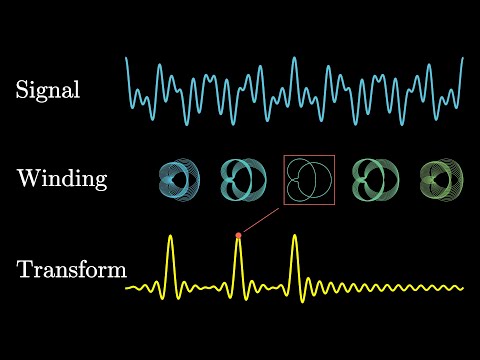
⇒ Formula allowing us to decompose a signal into its individual frequencies and the frequency’s amplitude:Loading equation...⇒ FT transfers a signal from the time domain to the frequency domain:.gif?table=block&id=27f05d07-7e22-4263-bbbf-a62fd82f49d6&cache=v2)
Function Loading equation...is first resolved into its Fourier series: a sum of sinusoidal waves. These sinusoids are then spread across the frequency spectrum and represented as peaks (Dirac delta functions) in the frequency domain. The function's frequency domain representationLoading equation...is the collection of these peaks. - Video on the FT:
Discrete Fourier Transform
- Creating a spectrogram is a digital process.
- Loading equation...be the continuous signal which is the source of the data.
- Loading equation...samples be denotedLoading equation....
⇒ We actually use Discrete Fourier Transform.⇒ DFT is the equivalent of the continuous FT for signals known only atLoading equation...instants separated by sample timesLoading equation....⇒ Let:⇒ Since the integrand exists only at the sample pointsLoading equation...:Loading equation...⇒ We may write this equation in matrix form asLoading equation...Loading equation...
Example #1
- Let the continuous signal be
- E.g.: Loading equation...,Loading equation...,Loading equation...,Loading equation....
Loading equation...
Example signal for DFT. ⇒ Let us sampleLoading equation...atLoading equation...times per second (i.e. sampling rate isLoading equation...) fromLoading equation...toLoading equation....⇒ Values of the discrete samples givenLoading equation...,Loading equation...:Loading equation...⇒ DFT isLoading equation...Loading equation...
DFT of four point sequence ( Loading equation...isLoading equation...in our case). - E.g.:
Example #2
- Consider the following signal with the frequency of Loading equation...:
- NB: amplitude spectrum is mirroring.
- Q: Why?A: We know thatLoading equation...Then note the following:Loading equation...
- Q: Why?
Loading equation...
⇒ DFT results in a sequence of complex numbers, so the amplitude is computed as the following:Loading equation...⇒ We get this graph:
- NB: amplitude spectrum is mirroring.
Discrete Fourier Transform Errors & Short-time Fourier Transform
- DFT is only an approximation since it provides only for a finite set of frequencies.⇒Loading equation...2 main types of DFT errors: aliasing and leakage.
Aliasing
- If the initial samples are not sufficiently closely spaced to represent high-frequency components present in the underlying function, then the DFT values will be corrupted by aliasing:
- Q: How to cope with aliasing?
- If possible, increase the sampling rate.
- Otherwise, pre-filter the signal in order to minimize its high-frequency spectral content.
A:
Leakage
- FT requires integration over the interval Loading equation...or over an integer number of cycles of the waveform.
- E.g.: consider case of input signal which is a sinusoid with a fractional number of cycles in Loading equation...data samples:
Leakage for Loading equation...toLoading equation...(Loading equation...isLoading equation...in our case).⇒ Might have expected the DFT to give an output at just the quantized frequencies either side of the true frequency. This certainly does happen but we also find non-zero outputs at all other frequencies.⇒ This effect, known as leakage, arises because we are effectively calculating the Fourier series for the waveform, which has major discontinuities, hence other frequency components:
⇒ We attempt to complete DFT over a non-integer number of cycles of the input signal.⇒ Might expect the transform to be corrupted in some way. - E.g.: consider case of input signal which is a sinusoid with a fractional number of cycles in
- Most sequences of real data are much more complicated than the sinusoidal sequences that we considered.
- NB:
- Loading equation...is the Hamming window.
- Loading equation...is the Hanning window.
- These window functions taper the samples towards zero values at both endpoints, ⇒ There is no discontinuity with a hypothetical next period (or very little, in the case of Hanning window).⇒ Leakage of spectral content away from its correct location is much reduced:
Leakage is reduced using a Hanning window.
⇒ It will not be possible to avoid discontinuities when using a finite number of points from the sequence in order to calculate the DFT.⇒ To cope with leakagre, we use one of the window functions that have the following form:Loading equation...Loading equation...Short-time Fourier transform divides a longer time signal into shorter segments of equal length and then computes the Fourier transform separately on each shorter segment:
⇒
- NB:
Fast Fourier Transform
- Time taken to evaluate a DFT on a digital computer depends on the number of multiplications involved. ⇒ This number is related toLoading equation...(matrix multiplication of a vector), whereLoading equation...is the length of the transform.⇒ For most problems,Loading equation...is chosen to be at leastLoading equation...in order to get a reasonable approximation.⇒ Сomputational speed becomes a major consideration.
- Highly efficient computer algorithms for estimating DFT have been developed since the mid-Loading equation...'s.
- It’s easy to realize that the same values Loading equation...are calculated many times as the computation proceeds:
- Integer product Loading equation...repeats for different combinations ofLoading equation...andLoading equation....
- Loading equation...is a periodic function with onlyLoading equation...distinct values.
- Integer product
⇒ These are known as Fast Fourier Transform (FFT) algorithms.⇒ They rely on the fact that the standard DFT involves a lot of redundant calculations.⇒ Re-writeLoading equation...asLoading equation... - It’s easy to realize that the same values
Spectrogram Generation
- Algorithm:
- Divide the signal into overlapping windows.
- Apply a window function (filter) to each window to combat leakage.
- Apply the Fast Fourier Transform (FFT) to each filtered window.
- Compute the square of the complex norm for each window (this is how the amplitude is calculated).
- Obtain a symmetrical vector, so only keep half of it.
- The higher you go in the column, the higher the frequencies represented, and vice versa.
- The brightness of the color indicates how strong a particular frequency is at that moment.
- E.g.: Yellow at the bottom represents a bass sound, while higher up represents a high-pitched sound.
Loading equation...By repeating these steps for all windows, we obtain a spectrogram, where each column is the result of all five steps applied to a single window.
Spectrogram Alternatives
- Spectrogram visualizes effectively many pertinent features of speech signals.
Windowed speech signal. 
Power spectrum of the speech segment. ⇒ Can observe events over time, changes inLoading equation...and also some features of the spectral envelope.⇒ But it has drawbacks as, by directly looking at power spectra, we don’t really see anything informative.⇒ Not a particularly efficient representation in terms of number of coefficients: the spectrum has a large number of coefficients in comparison to the amount of information which we are after.⇒ Typically we would like to have information of the formant locations and amplitudes.⇒ This could be represented by just a handful of coefficients.
- Logarithmic spectrum is a much more accessible representation:
- It’s not only more visual, but importantly, the logarithm approximates roughly the sensitivity of the ear, such that logarithmic spectra can be used to assess auditory importance of spectral features.
- Logarithmic spectrum visualizes spectral content such that the magnitude of values is approximately uniform throughout the spectrum.
- Only exception is zeros and other very small values in the magnitude spectrum.
- Q: How to deal with zeros?A: Instead ofLoading equation..., we can useLoading equation..., whereLoading equation...is a small positive number.⇒ Output will then never go lower than a thresholdLoading equation....⇒ In addition, we can integrate (or sum) neighboring frequencies, for example asLoading equation...whereLoading equation...is a scalar. The likelihood that all three coefficients,Loading equation...,Loading equation..., andLoading equation..., are all simultaneously near zero is much smaller than that one of them is near zero.
⇒ Give negative infinities or arbitrarily large negative values in the log spectrum.⇒ Such values are "difficult" for visualizations, and they are inconsequential for auditory perception.⇒ Can be often ignored.⇒ However, for computations in the log-spectrum, arbitrarily large negative values are a problem. - Q: How to deal with zeros?
Log-spectrum of speech segment. - It’s not only more visual, but importantly, the logarithm approximates roughly the sensitivity of the ear, such that logarithmic spectra can be used to assess auditory importance of spectral features.
Cepstrum
- Log-spectrum reveals a rich structural composition of the analyzed signal. ⇒ We see harmonic structure inherent in the signal, primarily arising from its fundamental frequency.⇒ Observing the log-spectrum at a broader scale uncovers a pattern of peaks and valleys.⇒ Signal peaks in log-spectrum are known as formants and can be used to uniquely identify all vowels.⇒ Quantifying these macro-level structures is important.
Illustration of the log-spectrum showing harmonic peaks and valleys* 
Detailed view of formant structures within the log-spectrum* ⇒ One way of evaluating such structures is to utilize the concept of the cepstrum.
- Cepstrum is a tool for investigating periodic structures in frequency spectra.
- Apply analysis windowing to the signal.
- Apply time-frequency transform (typically the Discrete Fourier Transform)
- Here we translate the time-domain signal into the frequency domain. ⇒ Unveil the signal's frequency components.
- Here we translate the time-domain signal into the frequency domain.
- Take the logarithm of the absolute value.
- Highlight the characteristics that define the signal's unique sound properties. ⇒ Accentuate harmonic and formant structures of the frequency-domain signal.
- Highlight the characteristics that define the signal's unique sound properties.
- Apply second time-frequency transform (typically Discrete Cosine Transform (DCT)).
- Reveal the quefrency domain. ⇒ Provide insights into the temporal structures embedded within the frequency domain.
- Reveal the quefrency domain.
⇒ Algorithm to get the cepstrum is as the following:
Look from left to right, top to bottom.
- It is worth repeating that the cepstrum involves two time-frequency transforms.⇒ Cepstrum of a time-signal is therefore in some sense similar to the time-domain.⇒ x-axis of a cepstrum is known as the quefrency-axis and it is expressed typically in the unit seconds.⇒ Through this lens, we gain the ability to distinguish and characterize the nuanced aspects of signals.
Features
- Cepstrum has two features:
- Low quefrencies contain information about the slowly-changing features of the log-spectrum.
- Interpretation of formant information in the cepstrum is, however, non-trivial.
- E.g.: locations of the formants, on the frequency-axis, are encoded in the cepstrum, but the information is distributed over several coefficients such that extracting that information is not easy.
⇒ Information of the formants will lie at the low-quefrency end of the cepstrum.
- Interpretation of formant information in the cepstrum is, however, non-trivial.
- Cepstrum is the harmonic structure of the log-spectrum.
- Recall that the fundamental frequency is visible as a comb-structure in the log-spectrum.
- Assume that fundamental frequencies Loading equation...are in the rangeLoading equation...toLoading equation...Hz.⇒ Corresponding peak in the cepstrum should lie at quefrencyLoading equation...and range fromLoading equation...toLoading equation...milliseconds.
- Just need to find the highest peak of the cepstrum in the appropriate quefrency-range.
- E.g.: in the cepstrum above, the peak is near quefrency Loading equation...ms. It corresponds to a fundamental frequency ofLoading equation.... That fundamental frequency is clearly visible also in the log-spectrum above, where the comb-structure has peaks at approximately multiples ofLoading equation....
- E.g.: in the cepstrum above, the peak is near quefrency
⇒ Comb-structure, in turn, is a periodic structure.⇒ Fourier transform is an excellent tool for extracting such structures.⇒ Can expect to see a peak in cepstrum at quefrency corresponding to pitch-period length (in seconds)⇒ Estimating the fundamental frequency in the cepstrum is very simple and relatively robust. - Assume that fundamental frequencies
- Recall that the fundamental frequency is visible as a comb-structure in the log-spectrum.
- Low quefrencies contain information about the slowly-changing features of the log-spectrum.
MFCCs
Mel-Frequency Cepstral Coefficients
- Cepstrum is good for extracting envelope and Loading equation...-information.⇒Loading equation...problem: it has a large number of coefficients for a little amount of information.
Down-sampling the log-spectrum
- Envelope information is about the slowly-varying shape of the log-spectrum. ⇒ We could try to extract that by a simple downsampling.
- Loading equation...problem: power-spectrum can sometimes have arbitrarily small values.⇒ In the log-spectrum translate to negative near-infinite values.⇒ Any information extraction in the log-domain would therefore be susceptible for bias to negative infinite.
- Loading equation...solution: apply smoothing in the power-spectrum.
- Could use a FIR-filter Loading equation..., or more generally, a triangular shape:
- Achieves this with a low number of coefficients. ⇒ Reasonably efficient model of the envelope.
- Loading equation...Downside: information does not reflect the importance of features for humans.⇒ Taking log-transform does map magnitudes to a perceptual scale, but the frequency scale is still not mapped to a perceptual domain.
⇒ Downsample, use analysis windowing, and apply the FIR-filterLoading equation...,Loading equation...:
⇒ Smoothed representation clearly catches the overall shape of the spectrum, which is the envelope. - Could use a FIR-filter
Mel-scale
- To improve the representation, we can include more information about auditory perception into the model.
- By introducing information about human perception, we focus the model on that part of the information which human listeners would find important.
- Log-spectrum already takes into account perceptual sensitivity on the magnitude axis, by expressing magnitudes on the logarithmic-axis. The other dimension is then the frequency axis.⇒ Idea: the human ear hears low frequencies well but does not distinguish high frequencies as clearly.⇒ We want to give more weight to low frequencies in the spectrogram and less to high frequencies, in order to store even less data.
- Above about Loading equation..., increasingly large intervals are judged by listeners to produce equal pitch increments.
- Popular formula to convert Loading equation...hertz intoLoading equation...mels is
- Corresponding inverse expression isLoading equation...
Loading equation... - Corresponding inverse expression is
⇒ Mel-scale describes the perceptual distance between pitches of different frequencies.⇒ That is the step fromLoading equation...toLoading equation...mel sounds as large as the step fromLoading equation...toLoading equation...mel.
- Popular formula to convert
- By taking points Loading equation..., using the above formula, we can find pointsLoading equation...whose perceptual distance is equal.⇒ To sample the log-spectrum with a perceptual scale, we pick samples at frequenciesLoading equation....⇒ However, if we would only pick samples at frequenciesLoading equation..., we would loose all the other information.⇒ We take a weighted sum of energies near the target frequencyLoading equation...asLoading equation...where scalarsLoading equation...are a weighting parameters usually chosen as triangular functions:Loading equation...
Loading equation...
. - Mel-envelope clearly models lower frequencies accurately, which is also where the all-important formants reside. That is, accuracy is concentrated on the important part, which is good. Higher frequencies, above Loading equation...in particular, are poorly modelled, but there is usually not too much energy anyway, so that is ok:
MFCCs
- Remaining issue with the log-melspectrum is however that neighbouring samples are highly correlated.
- Loading equation...problem: we cannot reduce accuracy more, because then we would start loosing accuracy of the formants.
- Say, we have a time-signal which has correlation over time. By taking the DCT, we obtain the spectrum of the signal, where samples are reasonably uncorrelated.
- Algorithm:
- Compute spectrogram of a segment of speech:
- Get mel-spectrogram by multipling spectrogram with mel-weighted filterbank.
- Take log, to get log mel-spectrogram.
- Take the DCT, to get MFCCs:
- Compute spectrogram of a segment of speech:
⇒ Similarly, we can take the DCT of the log-mel spectrum.⇒ This technique is known as the Mel-Frequency Cepstral coefficient (MFCC) representation. - Algorithm:
⇒ Use generic operation for decorrelating sequentially correlated data. - Say, we have a time-signal which has correlation over time. By taking the DCT, we obtain the spectrum of the signal, where samples are reasonably uncorrelated.
- MFCC is an abstract domain, which contains information about the spectral envelope of the speech signal.
- Not easy to interpret visually.
- Since it is designed to correspond to resemble perception in both magnitude and frequency axis, and to be roughly uncorrelated, it is efficient for computation.
- Beneficial properties of the MFCCs include:
- Quantifies the gross-shape of the spectral envelope which is important in identification of vowels.
- Though, it removes fine spectral structure—micro-level structure,—which is often less important. ⇒ Focuses on that part of the signal which is typically most informative.
- Though, it removes fine spectral structure—micro-level structure,—which is often less important.
- Computationally reasonably efficient calculation.
- Performance is well-tested and -understood.
- Quantifies the gross-shape of the spectral envelope which is important in identification of vowels.
- Some of the issues with the MFCC include:
- Choice of perceptual scale is not well-motivated.
- Scales such as the ERB or gamma-tone filterbanks might be better suited. However, these alternative filterbanks have not demonstrated consistent benefit, whereby the mel-scale has persisted.
- MFCCs are not robust to noise.
- Choice of triangular weighting filters Loading equation...is arbitrary and not based on well-grounded motivation.
- Alternatives have been presented, but they have not gained popularity due to minor effect on outcome.
- MFCCs work well in analysis but for synthesis they are problematic.
- It’s difficult to find an inverse transform—from MFCCs to power spectra—which is simultaneously unbiased (=accurate) and congruent with its physical representation (=power spectrum must be positive).
- Choice of perceptual scale is not well-motivated.